最长公共子序列
最长公共子序列

如图,有两个序列(长度可能不等)
如何求出它们的最长公共子序列的长度呢?
首先,假设前面一部分已经计算好了,正在匹配连红线部分,f[i][j]表示a[1..i]与b[1..j]的最长公共子序列
考虑以下3种情况:
a[x]=b[y]:f[x][y]=f[x-1][y-1]+1;a[x]!=b[y]:f[x][y]=max(f[x-1][y],f[x][y-1]);x=0||y=0:f[x][y]=0;
注:如果是求3个序列的最长公共子序列的方式与此类似
现在问题来了,我们如何得到一个最长公共子序列而仅仅不是简单的长度呢?其实我们离真正的答案只有一步之遥!
仍然考虑那个递推式,我们LCS(x,y)的值来源的三种情况:
(1) LCS(x – 1, y – 1) + 1如果Ax = By
这对应L(x,y) = L(x,- 1 y- 1)末尾接上Ax (2.1) LCS(x – 1, y) 如果Ax ≠ By且LCS(x – 1, y) ≥LCS(x, y – 1)
这对应L(x,y)= L(x – 1, y) (2.2) LCS(x, y – 1) 如果Ax ≠ By且LCS(x – 1, y) <LCS(x, y – 1)
这对应L(x,y) = L(x, y – 1) (3) 0 如果 x =0或者y = 0
这对应L(x,y)=空序列 
代码
#include <bits/stdc++.h>
using namespace std;
char a[500],b[500];
char num[501][501]; ///记录中间结果的数组
char flag[501][501]; ///标记数组,用于标识下标的走向,构造出公共子序列
void LCS(); ///动态规划求解
void getLCS(); ///采用倒推方式求最长公共子序列
int main()
{
int i;
strcpy(a,"ABCBDAB");
strcpy(b,"BDCABA");
memset(num,0,sizeof(num));
memset(flag,0,sizeof(flag));
LCS();
printf("%d\n",num[strlen(a)][strlen(b)]);
getLCS();
return 0;
}
void LCS()
{
int i,j;
for(i=1;i<=strlen(a);i++)
{
for(j=1;j<=strlen(b);j++)
{
if(a[i-1]==b[j-1]) ///注意这里的下标是i-1与j-1
{
num[i][j]=num[i-1][j-1]+1;
flag[i][j]=1; ///斜向下标记
}
else if(num[i][j-1]>num[i-1][j])
{
num[i][j]=num[i][j-1];
flag[i][j]=2; ///向右标记
}
else
{
num[i][j]=num[i-1][j];
flag[i][j]=3; ///向下标记
}
}
}
}
void getLCS()
{
char res[500];
int i=strlen(a);
int j=strlen(b);
int k=0; ///用于保存结果的数组标志位
while(i>0 && j>0)
{
if(flag[i][j]==1) ///如果是斜向下标记
{
res[k]=a[i-1];
k++;
i--;
j--;
}
else if(flag[i][j]==2) ///如果是斜向右标记
j--;
else if(flag[i][j]==3) ///如果是斜向下标记
i--;
}
for(i=k-1;i>=0;i--)
printf("%c",res[i]);
}例题
相似基因
题目背景
大家都知道,基因可以看作一个碱基对序列。它包含了 4 种核苷酸,简记作A,C,G,T。生物学家正致力于寻找人类基因的功能,以利用于诊断疾病和发明药物。
在一个人类基因工作组的任务中,生物学家研究的是:两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。
题目描述
两个基因的相似度的计算方法如下:
对于两个已知基因,例如 AGTGATG 和 GTTAG,将它们的碱基互相对应。当然,中间可以加入一些空碱基 -,例如:
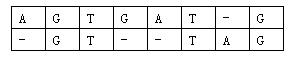
这样, 两个基因之间的相似度就可以用碱基之间相似度的总和来描述,碱基之间的相似度如下表所示:
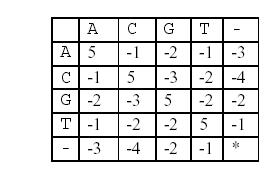
那么相似度就是: (−3)+5+5+(−2)+(−3)+5+(−3)+5=9 。因为两个基因的对应方法不唯一,例如又有:
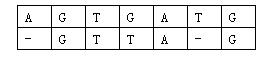
相似度为: (−3)+5+5+(−2)+5+(−1)+5=14 。规定两个基因的相似度为所有对应方法中,相似度最大的那个。
输入输出格式
输入格式:
共两行。每行首先是一个整数,表示基因的长度;隔一个空格后是一个基因序列,序列中只含 A,C,G,T 四个字母。 1≤ 序列的长度 ≤100 。
输出格式:
仅一行,即输入基因的相似度。
输入输出样例
输入样例 #1:
7 AGTGATG
5 GTTAG输出样例 #1:
14思路
变形的最长公共子序列
代码
#include <bits/stdc++.h>
using namespace std;
int f[105][105];
int cost[5][5]={5,-1,-2,-1,-3,
-1,5,-3,-2,-4,
-2,-3,5,-2,-2,
-1,-2,-2,5,-1,
-3,-4,-2,-1,0};
int ch(char x){
if (x=='A') return 0;
if (x=='C') return 1;
if (x=='G') return 2;
if (x=='T') return 3;
return 4;
}
int c(char x,char y){
int t1=ch(x);
int t2=ch(y);
return cost[t1][t2];
}
int main(){
int n,m;
char a[105],b[105];
cin>>n;
cin>>a+1;
cin>>m;
cin>>b+1;
for(int i=1;i<=n;i++) f[i][0]=f[i-1][0]+cost[ch(a[i])][4];
for(int i=1;i<=m;i++) f[0][i]=f[0][i-1]+cost[ch(b[i])][4]; //初始化千万别忘了,1和空配对
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
int t1=max(f[i-1][j]+c(a[i],'*'),f[i][j-1]+c(b[j],'*'));
f[i][j]=max(t1,f[i-1][j-1]+c(a[i],b[j]));
}
}
cout<<f[n][m];
return 0;
}
本作品采用知识共享署名-非商业性使用-相同方式共享 3.0 未本地化版本许可协议进行许可。
本文链接:https://hs-blog.axell.top/archives/13/
